Code

# cleaning
library(tidyverse)

# visualization
theme_set(theme_classic() +
            theme(panel.grid = element_blank(),
                  axis.text = element_text(size = 18),
                  axis.title = element_text(size = 18),
                  text = element_text(family = "Lato")))
library(patchwork)
library(ggeffects)
library(flextable)
library(GGally)
library(equatiomatic)

# data
library(palmerpenguins)

# analysis
library(car)
library(performance)
library(broom)
library(DHARMa)
library(MuMIn)
library(lmtest)

math notation

simple linear regression

\[ E[y_i] = a + bx_i \]

\[ var[y_i] = s^2 \]

generalized form:

\[ E[y_i] = a + bx_i \]

\[ var[y_i] = v(E[y_i]) \]

GLM structure using Gaussian example

random component

\[ Y_i \sim N(\mu_i, \sigma^2) \]

\[ Y_i \sim Normal(\mu_i, \sigma^2) \]

systematic component

\[ \eta_i = \sum^{p-1}_{n = 0}\beta_jx_{ij} \]

\[ \mu_i = \beta_0 + \beta x_i \]

link

\[ \eta = g(\mu_i) \]

GLM structure using binary example

random

\[ E(Y) = p \]

systematic

link

\[ \eta = g(p) = log(\frac{p_i}{1 - p_i}) \]

\[ log(\frac{p_i}{1 - p_i}) = \beta_0 + \beta_1 x_i \]

\[ Y_i \sim Binomial(p_i) \]

\[ \eta = logit(p_i) = log(\frac{p_i}{1 - p_i}) \]

binomial/bernoulli example

Code

set.seed(666)
lizard <- tibble(
  pushup = c(rep(1, 30), rep(0, 30)),
  distance = c(rnorm(n = 20, mean = 10, sd = 2), 
               rnorm(n = 20, mean = 20, sd = 2), 
               rnorm(n = 20, mean = 30, sd = 2))
) %>% 
  mutate(distance = round(distance, 1))

slice_sample(lizard, n = 10)

# A tibble: 10 × 2
   pushup distance
    <dbl>    <dbl>
 1      1      9.3
 2      1     11.7
 3      0     28.6
 4      0     33.7
 5      0     20.5
 6      0     28.8
 7      0     18.8
 8      1     14.3
 9      1     17.7
10      1     10.7

Code

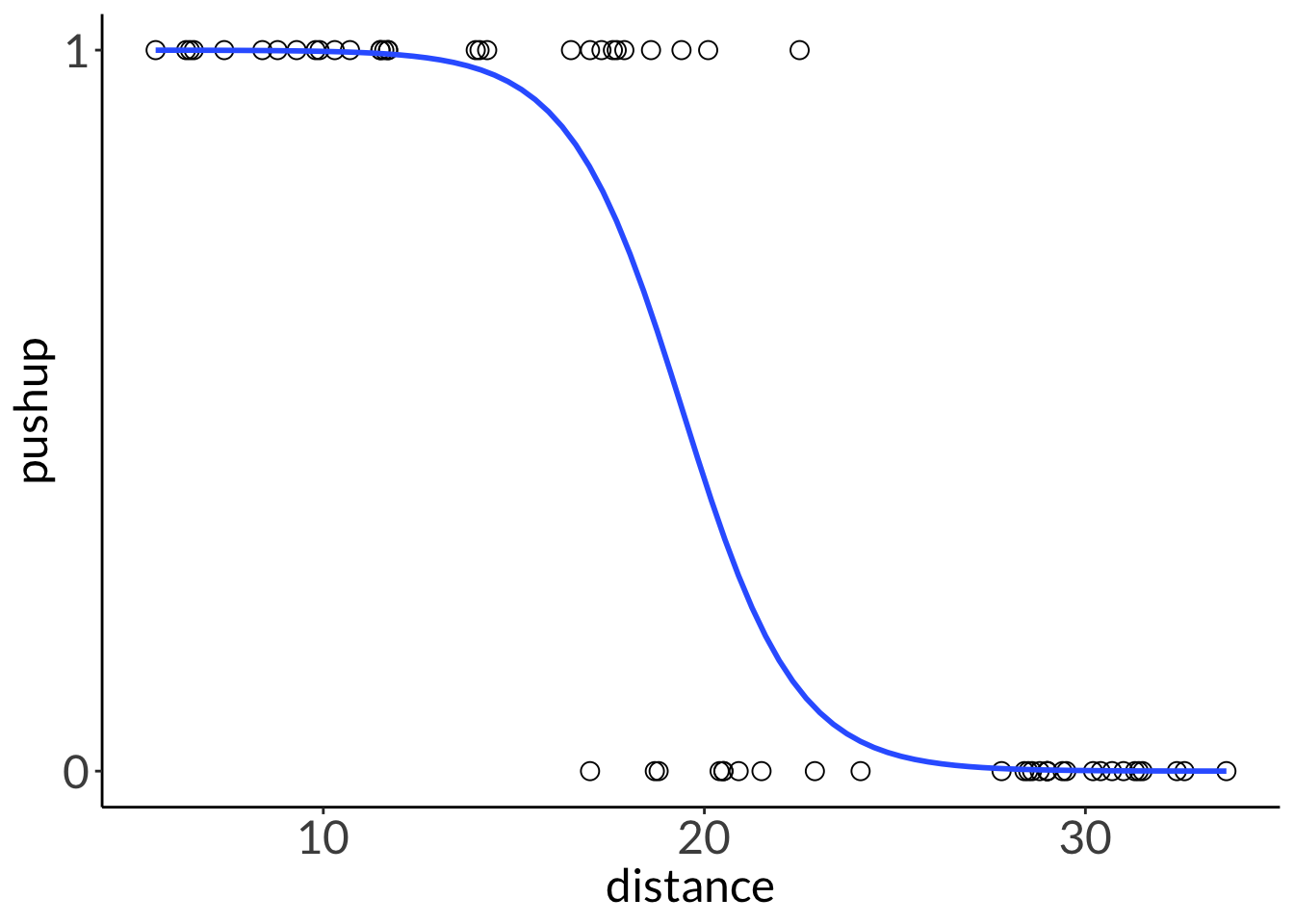
ggplot(lizard,
       aes(x = distance,
           y = pushup)) +
  geom_point(size = 3,
             shape = 21) +
  scale_y_continuous(limits = c(0, 1),
                     breaks = c(0, 1)) +
  geom_smooth(method = "glm",
              method.args = list(family = "binomial"),
              se = FALSE,
              linewidth = 1)

Code

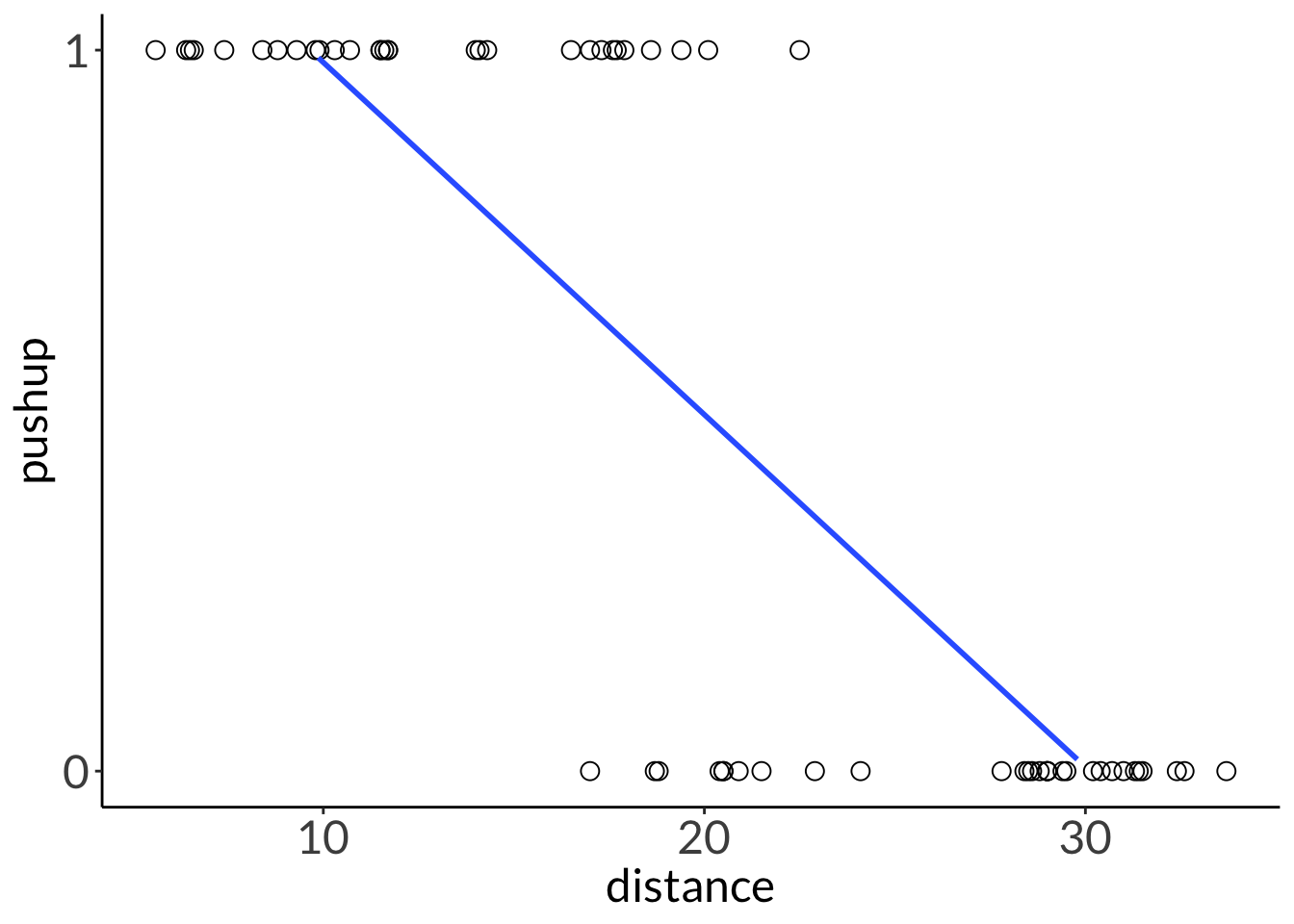
ggplot(lizard,
       aes(x = distance,
           y = pushup)) +
  geom_point(size = 3,
             shape = 21) +
  scale_y_continuous(limits = c(0, 1),
                     breaks = c(0, 1)) +
  geom_smooth(method = "lm",
              se = FALSE,
              linewidth = 1)

Code

liz_mod <- glm(pushup ~ distance,
               data = lizard,
               family = "binomial")

summary(liz_mod)


Call:
glm(formula = pushup ~ distance, family = "binomial", data = lizard)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)   
(Intercept)  13.0974     4.7342   2.767  0.00567 **
distance     -0.6741     0.2458  -2.743  0.00609 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 83.178  on 59  degrees of freedom
Residual deviance: 22.717  on 58  degrees of freedom
AIC: 26.717

Number of Fisher Scoring iterations: 8

Code

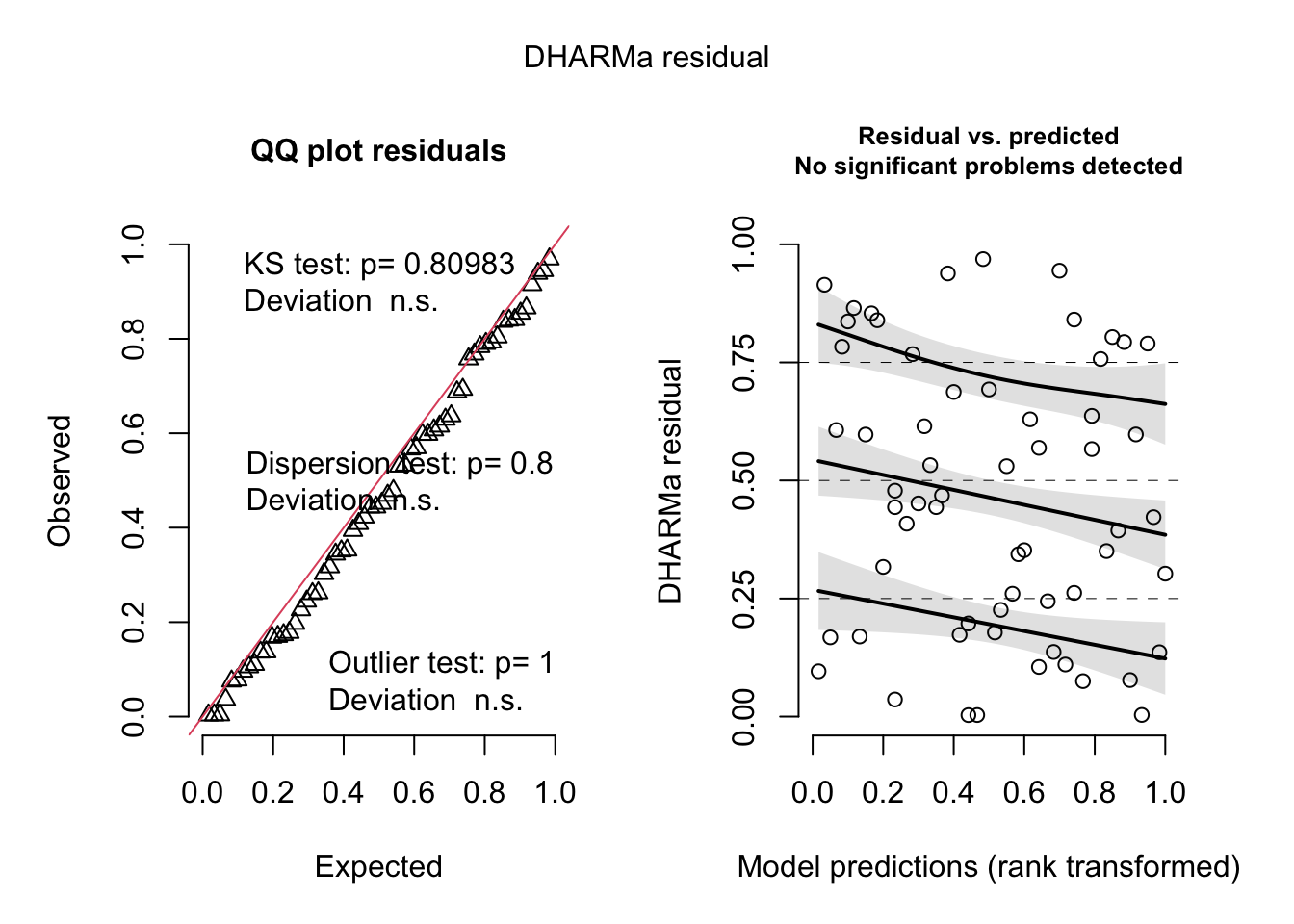
simulateResiduals(liz_mod) %>% plot()

Code

confint(liz_mod)

                2.5 %     97.5 %
(Intercept)  6.572132 25.5395134
distance    -1.319798 -0.3373257

Code

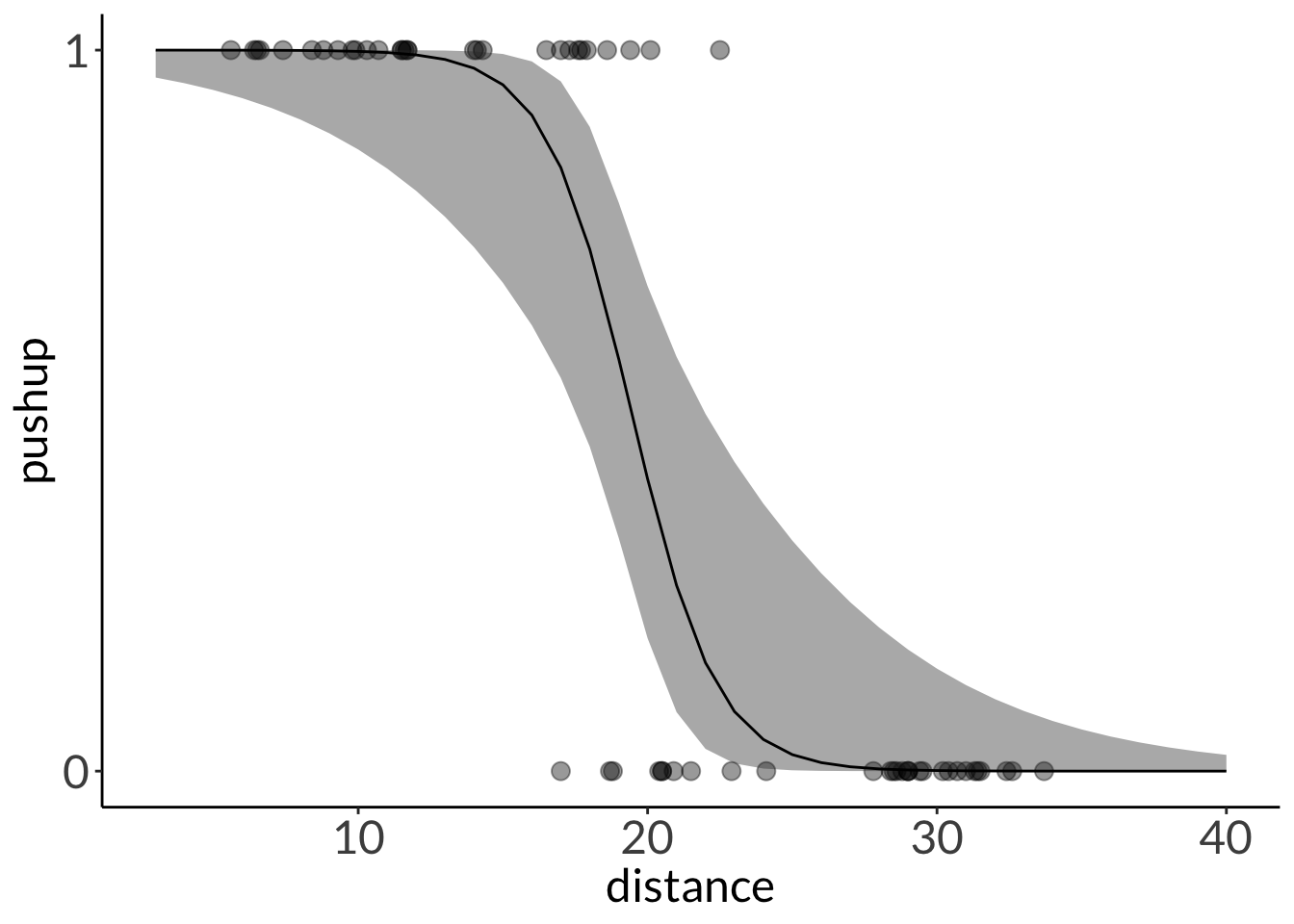
mod_preds <- ggpredict(liz_mod,
          terms = "distance [3:40 by = 1]") 

ggplot(lizard,
       aes(x = distance,
           y = pushup)) +
  geom_point(size = 3,
             alpha = 0.4) +
  geom_ribbon(data = mod_preds,
              aes(x = x,
                  y = predicted,
                  ymin = conf.low,
                  ymax = conf.high),
              alpha = 0.4) +
  geom_line(data = mod_preds,
            aes(x = x,
                y = predicted)) +
  scale_y_continuous(limits = c(0, 1),
                     breaks = c(0, 1))

Code

# what is the probability of a pushup at 20cm?
ggpredict(liz_mod,
          terms = "distance [20]")

# Predicted probabilities of pushup

distance | Predicted |     95% CI
---------------------------------
      20 |      0.41 | 0.18, 0.67

Code

# what is the probability of a pushup at 10cm?
ggpredict(liz_mod,
          terms = "distance [10]")

# Predicted probabilities of pushup

distance | Predicted |     95% CI
---------------------------------
      10 |      1.00 | 0.86, 1.00

Code

# what is the probability of a pushup at 30cm?
ggpredict(liz_mod,
          terms = "distance [30]")

# Predicted probabilities of pushup

distance | Predicted |     95% CI
---------------------------------
      30 |      0.00 | 0.00, 0.14

Code

# what is the probability of a pushup at 20cm?
predict(liz_mod, 
        newdata = data.frame(distance = 20), 
        type = "response")

       1 
0.405084

Code

r.squaredLR(liz_mod)

[1] 0.6349364
attr(,"adj.r.squared")
[1] 0.8465819

Code

gtsummary::tbl_regression(liz_mod)

Characteristic	log(OR)¹	95% CI¹	p-value
distance	-0.67	-1.3, -0.34	0.006
¹ OR = Odds Ratio, CI = Confidence Interval

Code

gtsummary::tbl_regression(liz_mod,
                          exponentiate = TRUE)

Characteristic	OR¹	95% CI¹	p-value
distance	0.51	0.27, 0.71	0.006
¹ OR = Odds Ratio, CI = Confidence Interval

Code

as_flextable(liz_mod)

	Estimate	Standard Error	z value	Pr(>\|z\|)
(Intercept)	13.097	4.734	2.767	0.0057	**
distance	-0.674	0.246	-2.743	0.0061	**
Signif. codes: 0 <= '*' < 0.001 < '' < 0.01 < '*' < 0.05

(Dispersion parameter for binomial family taken to be 1)
Null deviance: 83.18 on 59 degrees of freedom
Residual deviance: 22.72 on 58 degrees of freedom

negative binomial example

Code

set.seed(666)
nbinom_df <- bind_cols(
  size1 = rnbinom(mu = 10, size = 1, n = 100),
  size10 = rnbinom(mu = 10, size = 10, n = 100),
  size100 = rnbinom(mu = 10, size = 100, n = 100)
)

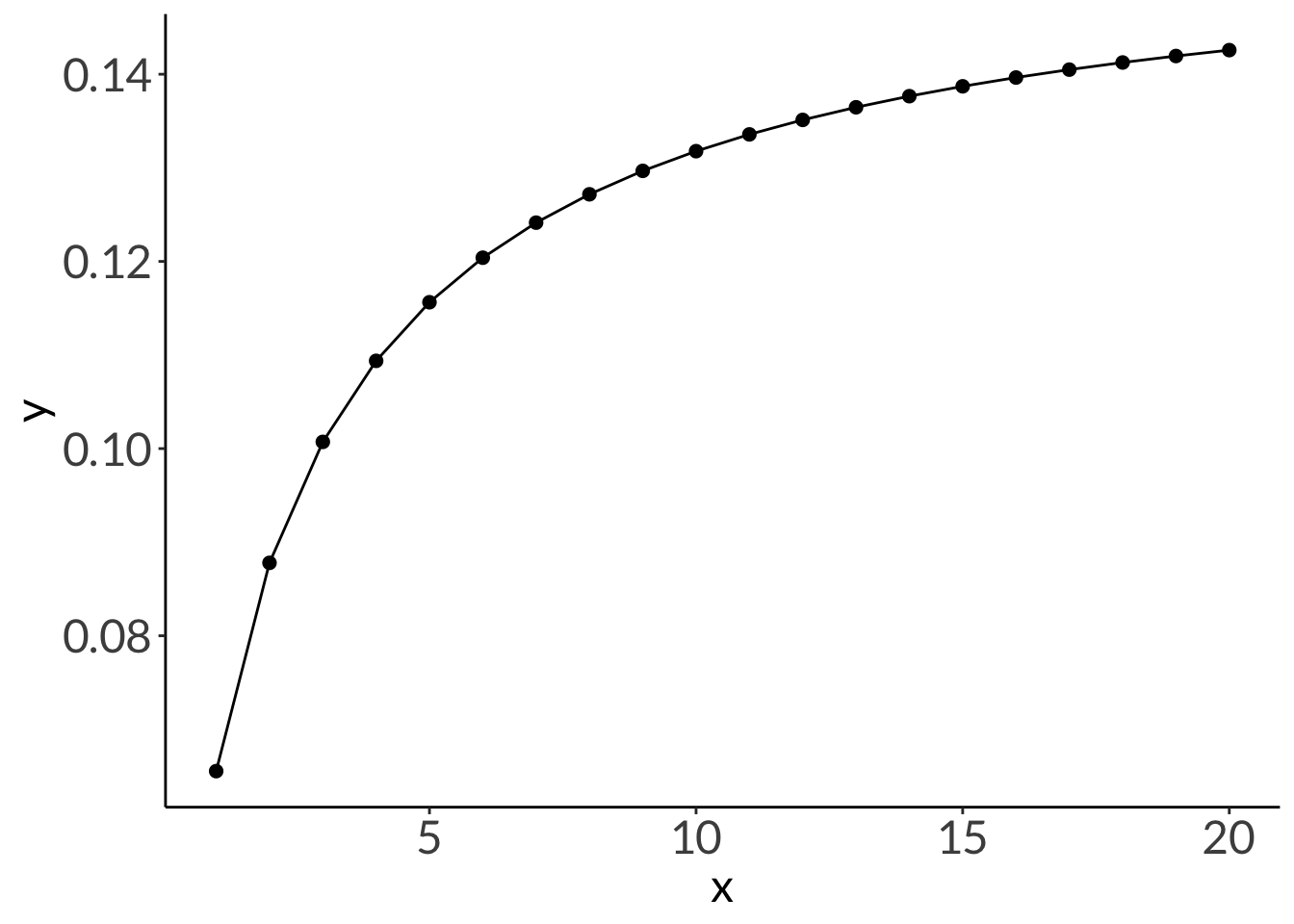
ggplot(data.frame(x = 1:20), aes(x)) +
  stat_function(geom = "point", n = 20, fun = dnbinom, args = list(mu = 4, x = 5), size = 2) +
  stat_function(geom = "line", n = 20, fun = dnbinom, args = list(mu = 4, x = 5))

Code

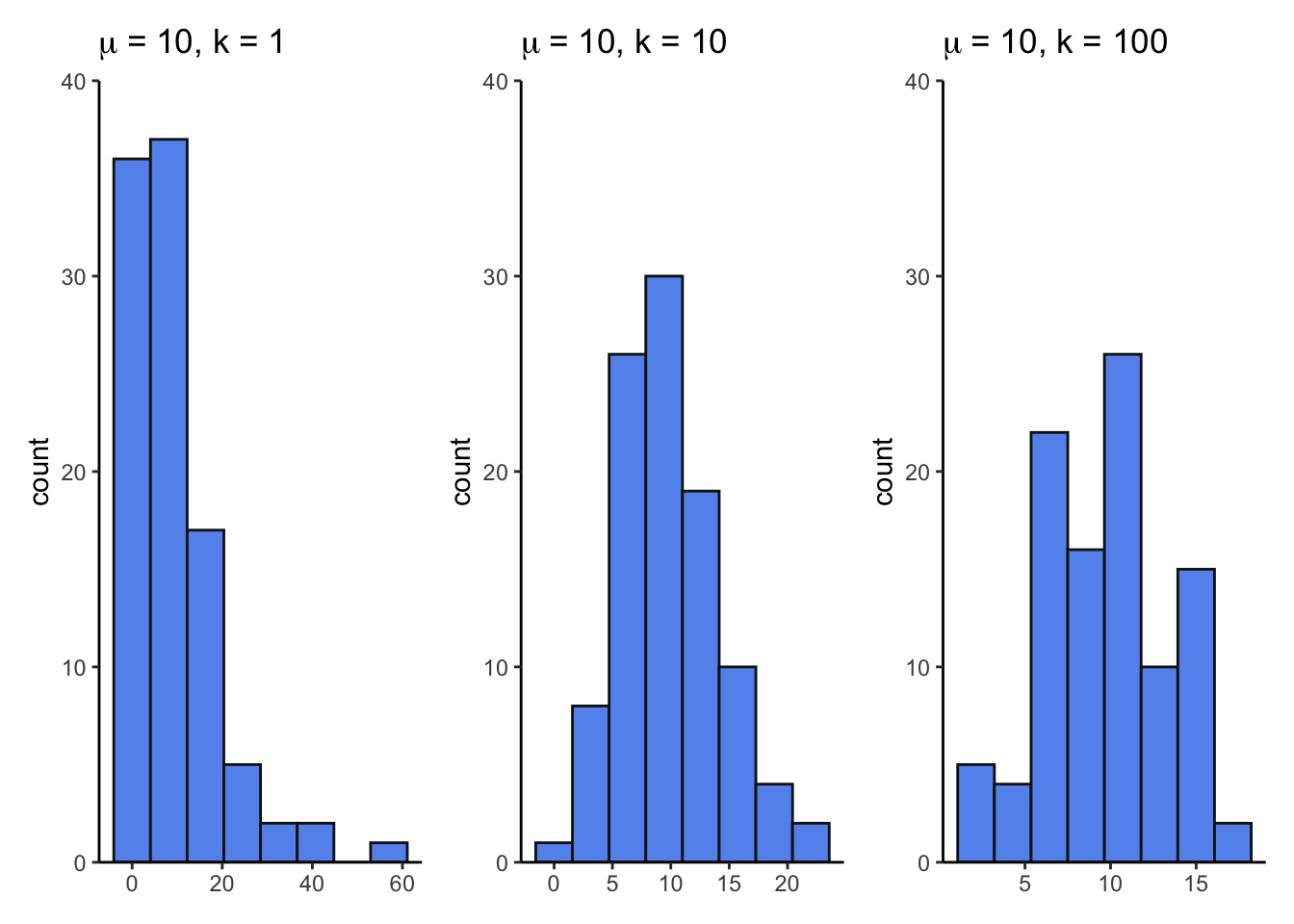
size1 <- ggplot(nbinom_df, aes(x = size1)) +
  geom_histogram(bins = 8, fill = "cornflowerblue", color = "grey8") +
  scale_y_continuous(expand = c(0, 0), limits = c(0, 40)) +
  theme_classic() +
  labs(title = expression(mu~"= 10, k = 1")) +
  theme(axis.title.x = element_blank())

size10 <- ggplot(nbinom_df, aes(x = size10)) +
  geom_histogram(bins = 8, fill = "cornflowerblue", color = "grey8") +
  scale_y_continuous(expand = c(0, 0), limits = c(0, 40)) +
  theme_classic() +
  labs(title = expression(mu~"= 10, k = 10")) +
  theme(axis.title.x = element_blank())

size100 <- ggplot(nbinom_df, aes(x = size100)) +
  geom_histogram(bins = 8, fill = "cornflowerblue", color = "grey8") +
  scale_y_continuous(expand = c(0, 0), limits = c(0, 40)) +
  theme_classic() +
  labs(title = expression(mu~"= 10, k = 100")) +
  theme(axis.title.x = element_blank())

size1 + size10 + size100

poisson example

Code

set.seed(666)
pois_df <- bind_cols(
  lambda1 = rpois(lambda = 1, n = 100),
  lambda5 = rpois(lambda = 5, n = 100),
  lambda20 = rpois(lambda = 20, n = 100)
)

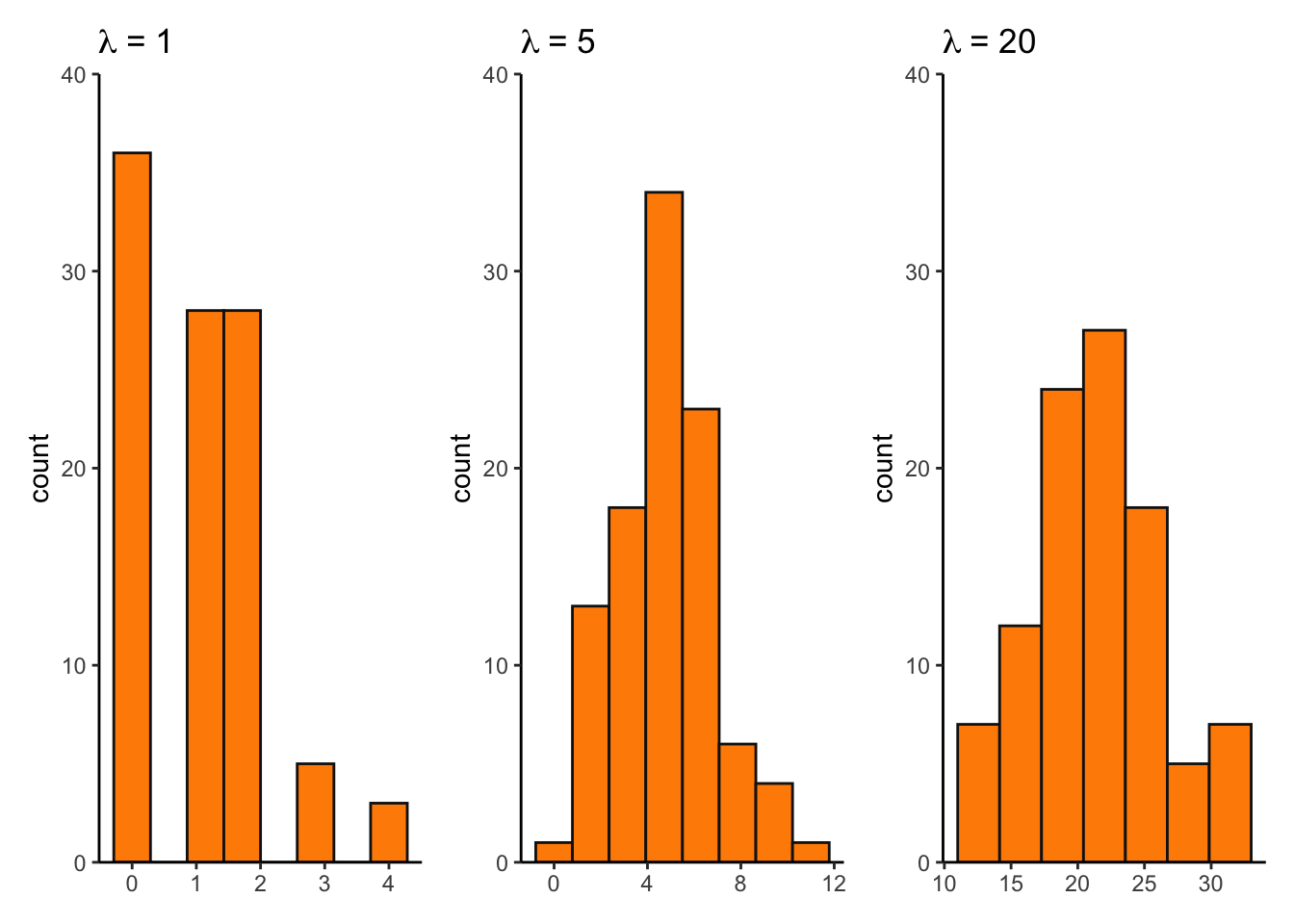
lambda1 <- ggplot(pois_df, aes(x = lambda1)) +
  geom_histogram(bins = 8, fill = "darkorange", color = "grey8") +
  scale_y_continuous(expand = c(0, 0), limits = c(0, 40)) +
  theme_classic() +
  labs(title = expression(lambda~"= 1")) +
  theme(axis.title.x = element_blank())

lambda5 <- ggplot(pois_df, aes(x = lambda5)) +
  geom_histogram(bins = 8, fill = "darkorange", color = "grey8") +
  scale_y_continuous(expand = c(0, 0), limits = c(0, 40)) +
  theme_classic() +
  labs(title = expression(lambda~"= 5")) +
  theme(axis.title.x = element_blank())

lambda20 <- ggplot(pois_df, aes(x = lambda20)) +
  geom_histogram(bins = 8, fill = "darkorange", color = "grey8") +
  scale_y_continuous(expand = c(0, 0), limits = c(0, 40)) +
  theme_classic() +
  labs(title = expression(lambda~"= 20")) +
  theme(axis.title.x = element_blank())

lambda1 + lambda5 + lambda20

Citation

BibTeX citation:

@online{bui2024,
  author = {Bui, An},
  title = {Week 10 Figures - {Lectures} 17 and 18},
  date = {2024-06-03},
  url = {https://spring-2024.envs-193ds.com/lecture/lecture_week-10.html},
  langid = {en}
}

For attribution, please cite this work as:

Bui, An. 2024. “Week 10 Figures - Lectures 17 and 18.” June 3, 2024. https://spring-2024.envs-193ds.com/lecture/lecture_week-10.html.